Generative Adversarial Networks
For the Nantes Machine Learning
Meetup
By Hugo Mougard
On July, 3
Paper
- Title
- Generative Adversarial Nets
- Authors
- Ian Goodfellow, Jean Pouget-Abadie, Mehdi Mirza, Bing Xu, David Warde-Farley, Sherjil Ozair, Aaron Courville and Yoshua Bengio
- Conference
- NIPS 2014
- Citations
- 872
Overview
- Concept
- Implementation example
- Extensions
Concept
What we'll talk about
Generative networks. Trained on unlabelled data. Useful to build priors (ie word2vec).
“What I cannot create, I do not understand.”
Concept
Applied to images

Concept
Applied to text
Busino game camperate spent odea
In the bankaway of smarling the
SingersMay , who kill that imvic
Keray Pents of the same Reagun D
Manging include a tudancs shat "
His Zuith Dudget , the Denmbern
In during the Uitational questio
Divos from The ’ noth ronkies of
She like Monday , of macunsuer S
Solice Norkedin pring in since
ThiS record ( 31. ) UBS ) and Ch
It was not the annuas were plogr
This will be us , the ect of DAN
These leaded as most-worsd p2 a0
The time I paidOa South Cubry i
Dour Fraps higs it was these del
This year out howneed allowed lo
Kaulna Seto consficutes to repor
Concept
How it used to be done
- Conceive a generator network (CNN, RNN, …)
- Craft a problem-dependent loss function
- …
- Profit?
Concept
GANs
Generative Adversarial Networks use a network instead of a problem-specific loss.
Concept
GANs
Concept
Training
Minimax: train the two networks by maximizing opposite objectives
- maximize the efficiency of the discriminator given the data
- maximize the errors of the discriminator on generated data
- goto 1.
Concept
Discriminator training
$$ \underset{D}{\max} \underset{\mathcal{x \sim P_\mathcal{r}}}{\mathbb{E}} \left[\log\left(D(\mathcal{x})\right)\right] + \underset{\mathcal{\tilde{x} \sim P_\mathcal{g}}}{\mathbb{E}} \left[\log\left(1 - D(\mathcal{\tilde{x}})\right)\right] $$Concept
Discriminator training
$$ \underset{D}{\max} \color{red}{ \underset{\mathcal{x \sim P_\mathcal{r}}}{\mathbb{E}} \left[\log\left(D(\mathcal{x})\right)\right] } + \underset{\mathcal{\tilde{x} \sim P_\mathcal{g}}}{\mathbb{E}} \left[\log\left(1 - D(\mathcal{\tilde{x}})\right)\right] $$Maximize the probability $D(\mathcal{x})$ when the input is real data.
Concept
Discriminator training
$$ \underset{D}{\max} \underset{\mathcal{x \sim P_\mathcal{r}}}{\mathbb{E}} \left[\log\left(D(\mathcal{x})\right)\right] + \color{red}{ \underset{\mathcal{\tilde{x} \sim P_\mathcal{g}}}{\mathbb{E}} \left[\log\left(1 - D(\mathcal{\tilde{x}})\right)\right] } $$Minimize the probability $D(\mathcal{\tilde{x}})$ ($\max$ of $1 - p$) when the input is generated.
Concept
Generator training
$$ \underset{G}{\min} \underset{\mathcal{x \sim P_\mathcal{g}}}{\mathbb{E}} \left[\log\left(1 - D(\mathcal{\tilde{x}})\right)\right] $$Maximize the probability $D(\mathcal{\tilde{x}})$ ($\max$ of $1 - p$) when the input is generated.
Concept
Convergence
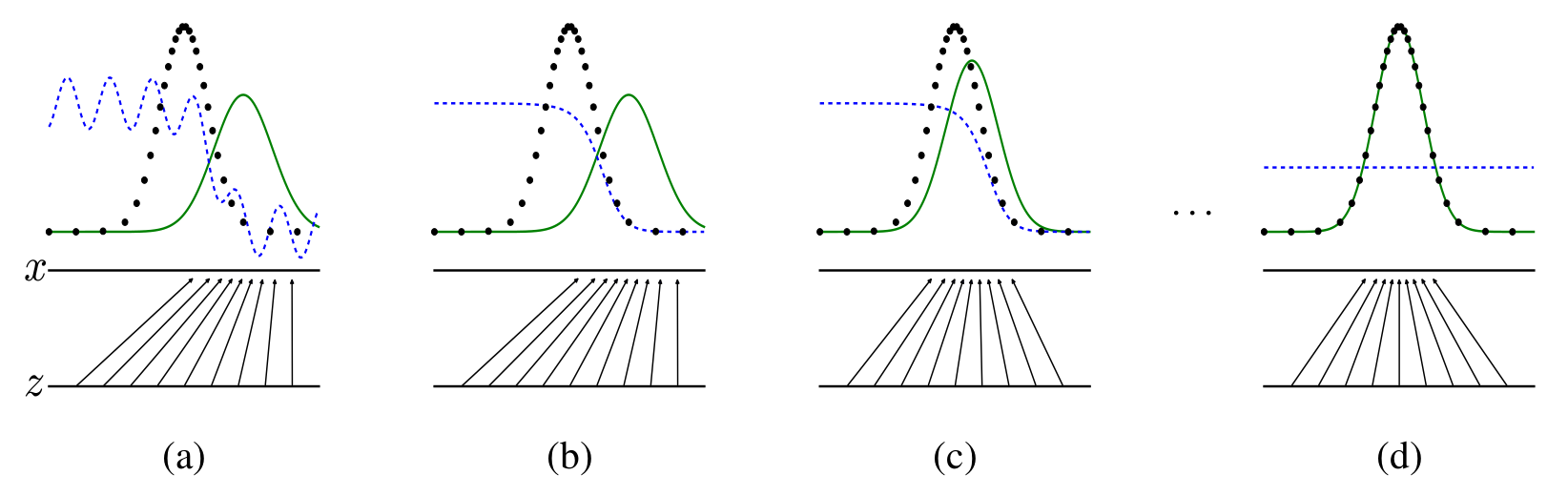
Final formulation
$$ \underset{G}{\min} \underset{D}{\max} \underset{\mathcal{x \sim P_\mathcal{r}}}{\mathbb{E}} \left[\log\left(D(\mathcal{x})\right)\right] + \underset{\mathcal{x \sim P_\mathcal{g}}}{\mathbb{E}} \left[\log\left(1 - D(\mathcal{\tilde{x}})\right)\right] $$Overview
- Concept
- Implementation example
- Extensions
Implementation example
DCGAN
- Title
- Unsupervised representation learning with deep convolutional GANs
- Authors
- Alec Radford, Luke Metz and Soumith Chintala
- Conference
- ICLR 2015
- Citations
- 415
Implementation example
DCGAN
Let's have a look at the DCGAN Torch code.
Implementation example
DCGAN
Overview
- Concept
- Implementation example
- Extensions
Extensions
Wasserstein GANs
GANs are extremely hard to train. WGANs fix that.
Extensions
Wasserstein GANs
Change the role of the discriminator:
- Before
- Output a probability of the data being real
- After
- Output a scalar representing how much the fake data distribution has to change to match the real one.
Extensions
Wasserstein GANs
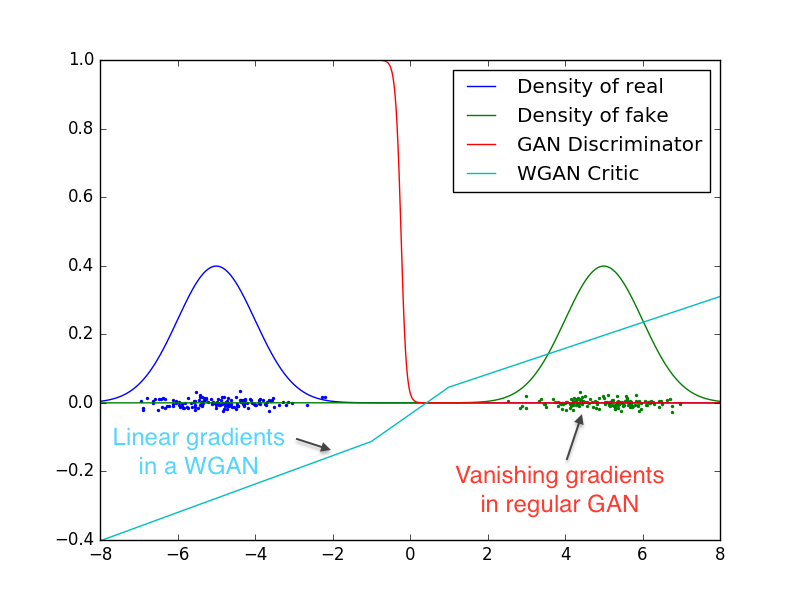
Extensions
Adversarially Learned Inference
Add an encoder from input to code to be able to query the generator.
Extensions
Adversarially Learned Inference
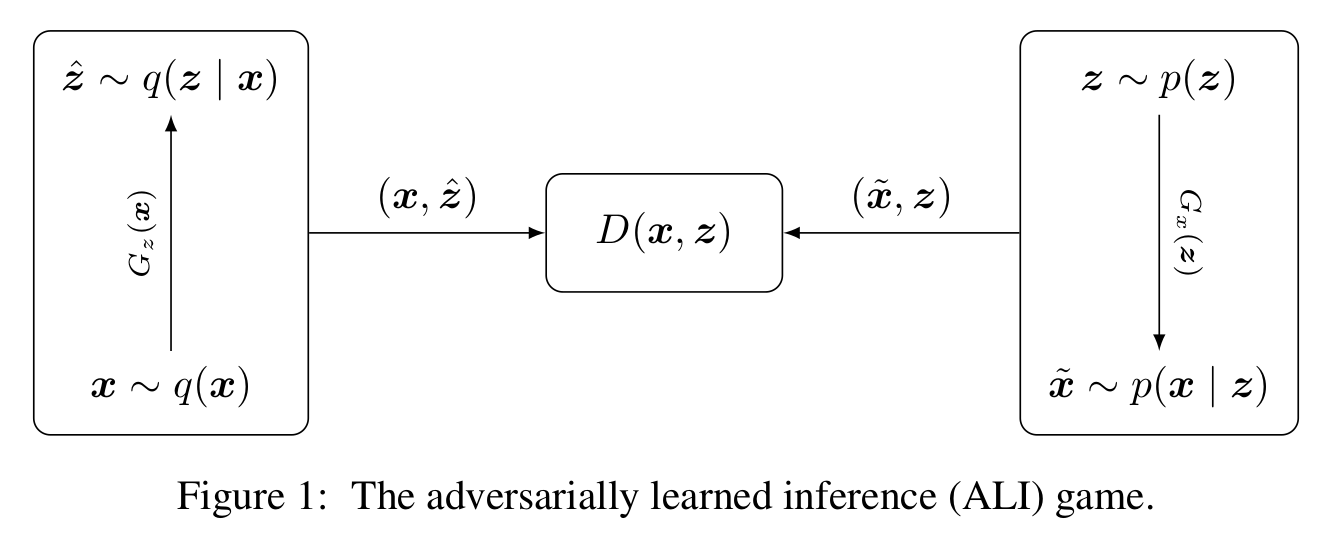
Extensions
Adversarially Learned Inference
The discriminator now distinguishes between couples $(x, z)$.
Extensions
Invertible Conditional GANs
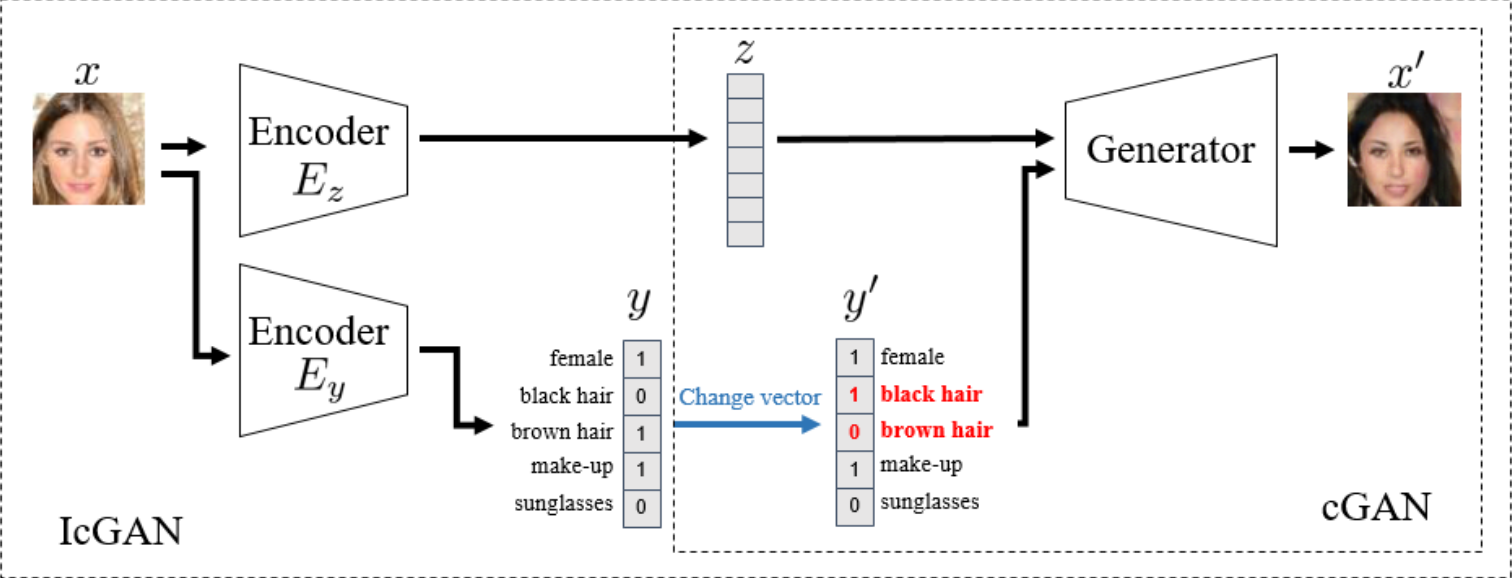
Extensions
Invertible Conditional GANs

Extensions
Improved Training of WGANs
Minor tweak on WGANs that allowed very easy training of GANs in multiple domains (text, image, …)
Conclusion
- Very promising paradigm
- Results in very good priors
- Becoming easier and easier to train
- Not limited to images and toy data anymore